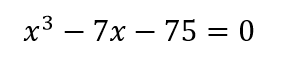GCSE Unit 2 | Use of a calculator is allowed |
Formulae

Questions
| 1. |
Four of the interior angles of a seven-sided polygon are 114o , 150o , 160o and 170o. The other three interior angles of this polygon are equal. Calculate the size of each of the other three interior angles. [5]
| ||
| 2. | (a) Express 144 as the product of its prime factors in index form. [3]
(b) Given that 60 = 22 x 3 x 5, find: (i) the highest common factor (HCF) of 144 and 60, [1] (ii) the lowest common multiple (LCM) of 144 and 60. [1]
| ||
| 3. | (a) Solve the inequality given below. [2]
7n < 5n + 11 (b) Give the largest integer value for n that satisfies this inequality. [1]
| ||
| 4. | A solution to the equation
Use the method of trial and improvement to find this solution correct to 1 decimal place.
| ||
| 5. | Carys has a Monday to Friday job and a weekend job. Working Monday to Friday and working weekends are independent events. In any given week, the probability that Carys works every day from Monday to Friday is 0.65 . The probability that she works both days during a weekend is 0.2 . (a) Complete the following tree diagram. [2]
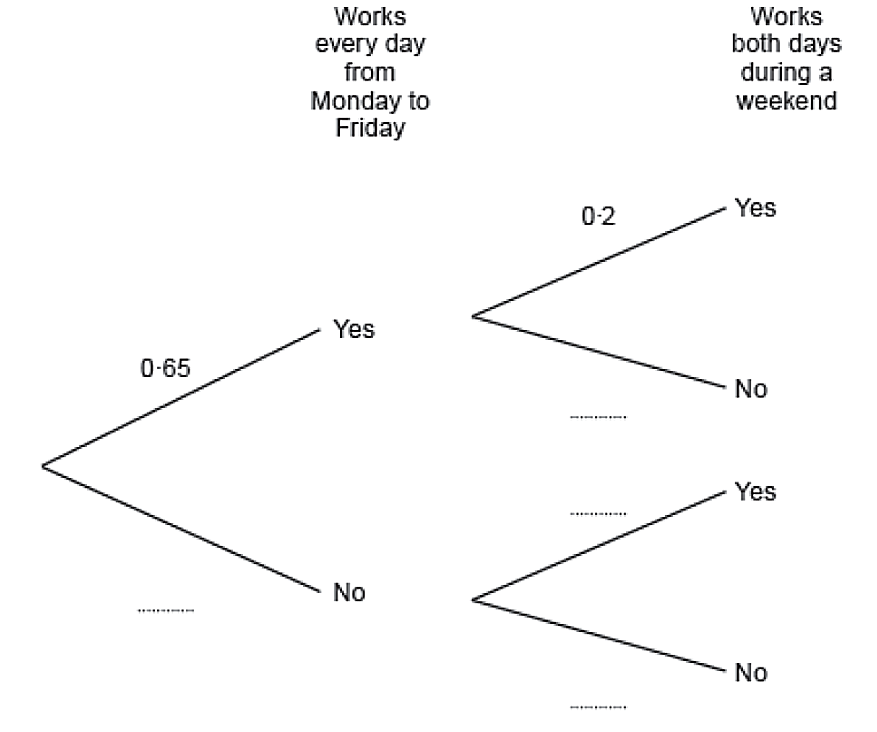 (b) Calculate the probability that next week Carys will work every day from Monday to Sunday. [2]
| ||
| 6. | An allotment has two rectangular flower beds A and B.
Flower bed A is x metres long and y metres wide.
The perimeter of flower bed A is 18 metres.
Use an algebraic method to calculate the area of flower bed B.
| ||
| 7. | Factorise x2 - x - 20, and hence solve x2 - x - 20 = 0 [3]
| ||
| 8. | A sketch of the graph of the straight line y = 7x + 2 is shown below.

(a) What are the coordinates of the point A, where the line cuts the y-axis?

(b) When h is equal to 1 unit, what is the value of k?

(c) Which of the following equations is an equation of a straight line that is perpendicular to y = 7x + 2?

| ||
| 9. |
 Calculate the length AD. [3] Find the size of the angle x. [5]
| ||
| 10. | (a) Make c the subject of the following formula. [2]
(b) Solve 3x2 + 4x - 18 = 0, giving your answers correct to two decimal places.
| ||
| 11. | ABCD is a rectangle, P, Q, R and S are the mid-points of the sides.
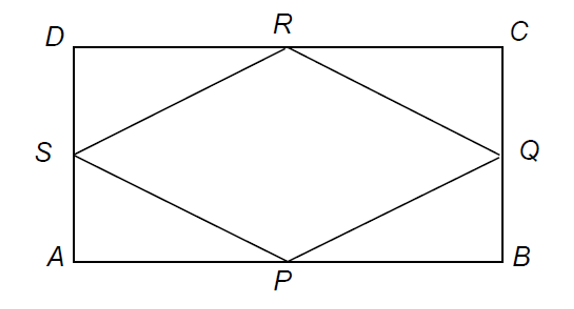 (a) Prove that triangles APS and CRQ are congruent. [3]
(b) Use your proof in part (a) to decide what is the special name given to the quadrilateral PQRS.
| ||
| 12. | The square and the sector of a circle shown below have equal areas.
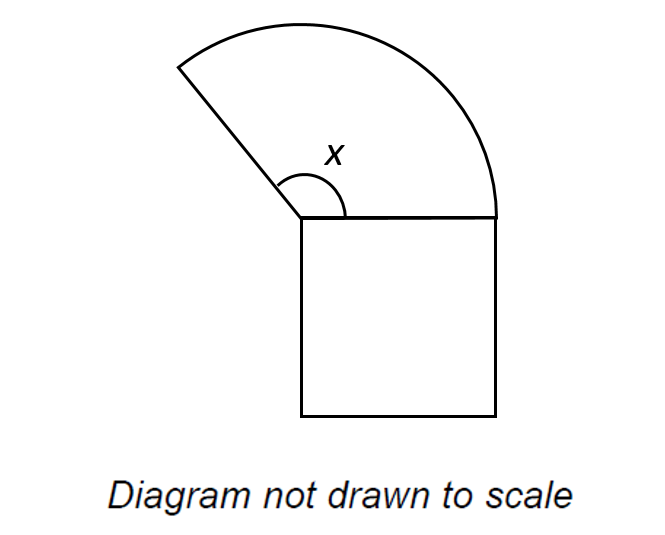 Calculate the size of angle x. [3]
| ||
| 13. | 
| ||
| 14. | 30 students in a Year 11 class have decided which subjects they are going to study next year.
The universal set ε contains all the students in the class. [2]
 (b) Given that a student, chosen at random, has decided to study French, what is the probability that this student has also decided to study German? [2]
| ||
| 15. | Circle the correct answer for each of the following questions.
(a) tan 30o is equal to,
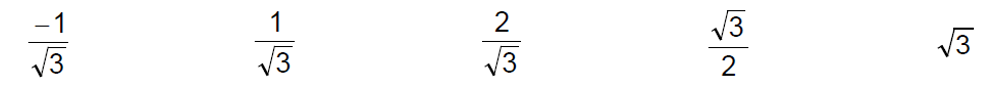 (b) cos 150o is equal to,
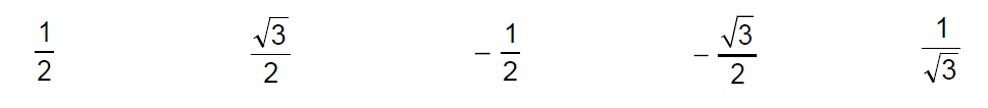 (c) The graph
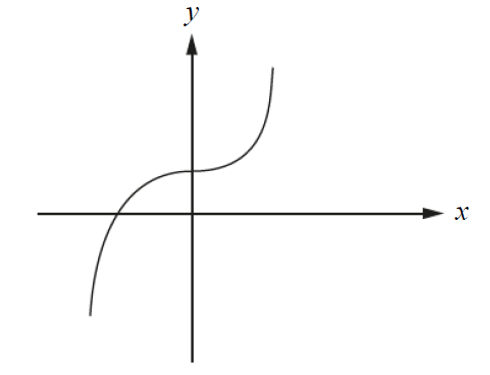 can be represented by the equation
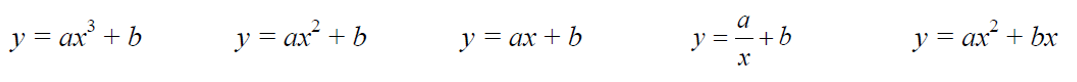
where a and b are both positive numbers.
| ||
| 16. | Using the axes below, sketch the graph of y = sin x + 3 for values of x from 0o to 360o. [2]

| ||
| 17. |
 Calculate the area of triangle ACD. [6]
| ||
| 18. | A factory produces a very large number of beads which are either coloured red or coloured blue. The beads are identical in all other respects. The probability of a randomly chosen bead being red is 0.7. The beads are randomly packed in boxes of 20 beads.
|