Introduction Weekly sessions




GCSE Unit 1

Use of a calculator not allowed

Formulae


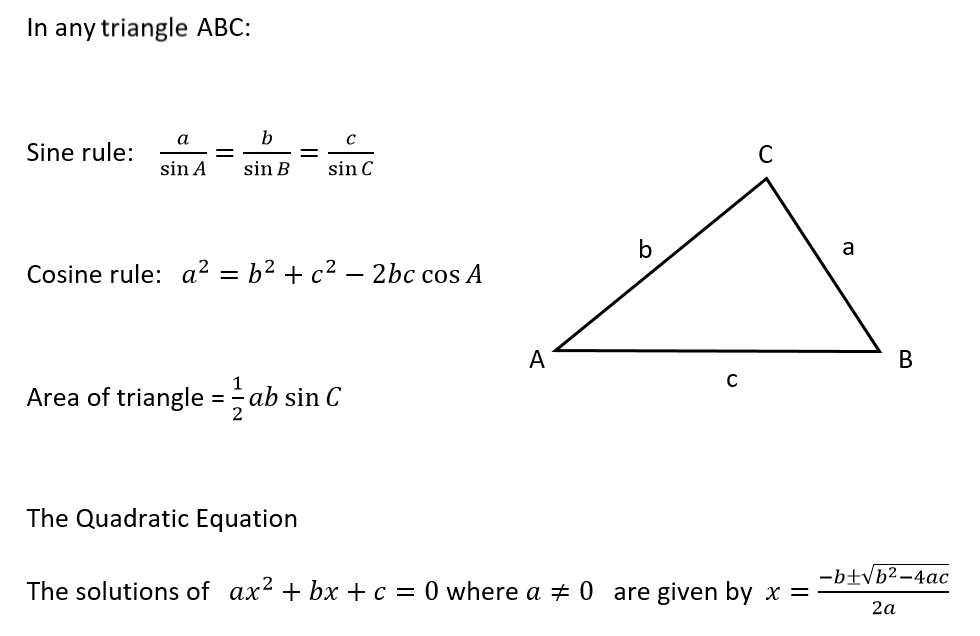
Questions

1. Mair either walks, cycles, travels by car or travels by bus to work each day. Her method of travel each day is independent of her method of travel on any other day.

The table below shows the probability for three of her methods of travel on any randomly chosen day.

(a) Calculate the probability that, on any randomly chosen day, she walks to work.     [2]

(b) What is the probability that, on any randomly chosen day, she either travelled to work by car or by bus?     [2]

(c) What is the probability that, in any randomly chosen week, Mair travelled to work by car on the Monday and by bus on the Tuesday?     [2]



    

2. The table below shows some of the values of y = x2 -3x -2 for values of x from -2 to 4.

Complete the table by finding the value of y for x = 2.

(b) On the graph paper below, draw the graph of y = x2 -3x -2 for values of x from -2 to 4.      [2]

(c) Using your graph, write down the two solutions of the equation x2 -3x -2 = 0 .
     Give your answers correct to 1 decimal place.      [1]

(d) By drawing a suitable line on your graph, write down the two solutions of the equation x2 -3x +1 = 0 .
     Give your answers correct to 1 decimal place.      [3]



    

3. (a) Use a ruler and a pair of compasses to construct an angle FGH of size 30o at point G.      [3]






(b) A regular polygon has interior angles of 135o.
     How many sides does this polygon have?      [3]


(c) Shape A is translated onto Shape B.

Which one of the following vectors describes the translation?
Circle your answer.      [1]



    

4. (a) Calculate the largest share when £400 is shared in the ratio 1:2:5     [2]

(b) A price of £63 includes VAT at a rate of 5%.
    What was the price before VAT was added?     [2]



    

5. Circle your answer in each of the following.

(a) The value of 2 -3 as a fraction in its simplest form is





              [3]


    

6. A six-sided dice was thrown repeatedly.
After every 100 throws, the cumulative number of sixes thrown was recorded.

(a) Complete the table below, which gives a summary of the results obtained.      [1]

(b) Draw a relative frequency diagram to show the information given in the table.      [1]

(c) From the table, which value gives the best estimate for the probability of throwing a six? You must give a reason for your choice.      [1]

(d) Do you think this is a fair dice? You must give a reason for your choice.      [1]



    

7. Find, in standard form, the value of

(a) (4.1 x 10 -5) x 3000,      [2]

(b) (1.5 x 103) ÷ (3 x 106).      [2]



    

8. The diagram shows the first four patterns of a sequence.

Find an expression for the number of squares in the nth pattern of the sequence.      [2]



    

9.



    

10. Given that y is inversely proportional to x2, and that y = 5 when x = 2,

(a) find an expression for y in terms of x.      [3]

(b) Use the expression you found in (a) to complete the following table.      [2]



    

11. A cuboid with a volume of 912cm3 has dimensions 4cm, (x + 2) cm and (x + 9) cm.

Show that x2 + 11x - 210 = 0.

Solve this equation and find the dimensions of the cuboid.
You must justify any decisions that you make.      [9]


    

12. Circle your answer in each of the following.

(a)      (2a3)4 is equal to

(b) Given that h2 = a2 + b2, then b is equal to

              [2]

    

13.

    

14. (a) The diagram shows a sketch of the graph y = f(x).
     The graph passes through the points (-2, 0) and (6, 0) and its highest point is at (2, 4).

Sketch the graph of y = f(x + 5) on the axes below.
You must indicate the coordinates of its highest point and the coordinates of the points of intersection of the graph with the x-axis.      [3]

(b) The diagram below on the left shows a sketch of the graph of y = x2.

Sketch the graph of y = -x2 + 3 on the axes on the right.
You must indicate the coordinates of the point where the curve crosses the y-axis.      [2]

(c) Explain why it is not possible to determine the translation used on the function g(x) in the diagram below.      [1]



    

15. The points A, B and C lie on the circumference of a circle.

The straight line PBT is a tangent to the circle.
AB = AC.
Angle CBP = x, where x is measured in degrees.



    

16. (a) When Anna shoots an arrow, the probability that she hits the target is 0.3
     Each attempt is independent of any previous shot.

(i) What is the probability that Anna hits the target for the first time on her third attempt?      [3]

(ii) Evaluate whether or not there is more than a 50% chance of Anna hitting the target exactly once on her first three attempts.      [3]



(b) Siôn selects two balls, at random, from a box containing 15 blue balls and 5 red balls.

He calculates that the probability of selecting two red balls is

What assumption has Siôn made for his answer to be correct?           [1]